The viscosity of a fluid means the resistance of the fluid to shear or angular deformation. In easy meaning, it is like a frictional force in a fluid which create resistance to flow. This frictional forces in fluid flow resulting from the cohesion and momentum interchange between molecules in the fluid. It is due to the viscous force that arises in the fluid.

A little bit of confusion can create between elastic forces and viscous forces but we will have to bear in mind that elastic force arises in solid but the viscous force arises in the fluid.
Following are some common terms and issues which need to be known to understand the viscosity clearly.
Viscous Force
Viscosity in Turbulent Flow
Viscosity is relatively low in turbulent flow. For this, the velocity of turbulent flow is relatively so high.
Viscosity in Ideal Fluid and Real Fluid
Ideal Fluid: It is such a fluid which is presumed to have no Viscosity. This is an idealized condition which doesn’t exist.
Real Fluid: In this fluid, the effect of viscosity is considered which results in the development of shear stresses between neighboring particles when they are moving in different velocities. Actually, all the fluid are real fluid because in fluid there will exist at least a minimum level of viscosity.
Absolute Viscosity
From Newton’s law of Viscosity, Shear stress on a fluid element layer is directly proportional to the rate of shear strain. Here, the constant is known as absolute viscosity or dynamic viscosity,
\[\tau=\mu\times\frac{du}{dy}\]
Here,
\[\mu= \frac{\text{Absolute Viscosity}}{\text{Dynamic Viscosity}}\]
\[\tau= \text{Shear Stress}\]
Kinematic Viscosity
It is defined as the ratio between, dynamic viscosity to the density of a fluid.
\[\gamma=\frac\mu\rho\]
Here, \[\gamma= \text{Kinematic Viscosity}\]
\[\rho= \text{Density}\]
Importance of Viscosity
- Viscosity is a critical property of hydraulic oil. Complete system performance and efficiency are the main parameters of hydraulic oil. These two parameters are affected by viscosity. Also for using valves and pumps viscosity is an important element.
- In lubrication, the viscosity is the most needed characteristic of lubricating oil. For greases, the viscosity is an important element too.
- If the temperature of the fluid is low then the viscosity is high, at that time oil cannot be pumped. On the other hand, if the temperature is high then the velocity of oil will be excessive, that means viscosity is so low and this can cause high friction in any pipe then wear.
- Viscosity is a measure of whether the flow is laminar or turbulent.
- By the help of Viscosity, we can know the behavior of viscosity which helps to design a machine in mechanical engineering, to build a ship, to work in marine condition.
- Because of high viscosity some fluid stay in steady condition. If there are no viscosity fluid would have no internal resistance and so it will flow forever before facing any barrier.
- From the behavior of viscosity with temperature, we can find whether the fluid is liquid or gas. For increasing the temperature the viscosity will increase for gas. On the other hand, increasing the temperature will decrease the Viscosity for Liquid.
{adselite}
Measurement of Viscosity
Absolute Viscosity
Stated it before, From Newton’s law of Viscosity, Shear stress on a fluid element layer is directly proportional to the rate of shear strain. Here, the constant is known as absolute viscosity or dynamic viscosity,
\[\tau=\mu\times\frac{\text{d}u}{\text{d}y}\]
Here, \[\mu=\text{Absolute viscosity/ Dynamic Viscosity/ Constant of proportionality}\]
\[\tau= \text{Shear Stress}\]
\[\frac{\text{d}u}{\text{d}y}=\text{ Velocity Gradient [Rate of change of velocity with respect to space]}\]
From Reynolds Number,
\[R= \frac{DV\rho}\mu\]
Here,
\[R= \text{Reynolds Number}\]
\[\rho= \text{Density of the fluid}\]
\[\mu= \frac{\text{Absolute Viscosity}}{\text{Dynamic Viscosity}}\]
\[D= \text{Diameter of the pipe}\]
\[V= \text{Velocity of the flow}\]
Kinematic Viscosity
From Absolute Viscosity,
\[\gamma=\frac\mu\rho\]
Here, \[\gamma= \text{Kinematic Viscosity}\]
\[\rho= \text{Density}\]
From Reynolds Number,
\[R= \frac{DV}\gamma\]
Here,
\[R= \text{Reynolds Number}\]
\[\gamma= \text{Kinematic Viscosity}\]
\[D= \text{Diameter of the pipe}\]
\[V= \text{Velocity of the flow}\]
Reynolds Number
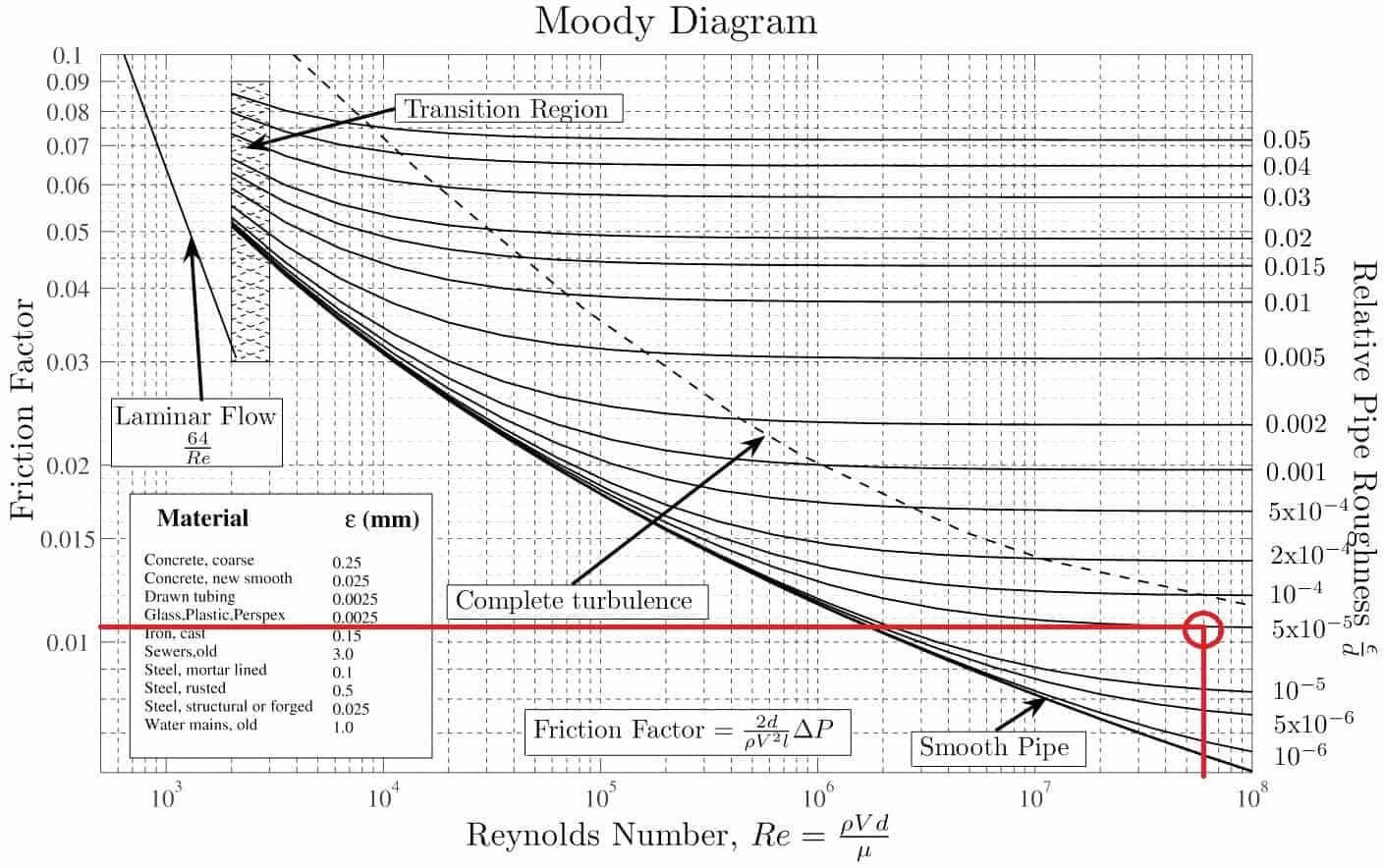
Reynolds Number can be found through Moody Diagram in where from relative roughness and friction factor we can find the Reynolds number.
Relative Pipe roughness is a parameter of the pipe used,
\[\text{Relative Pipe Roughness}= \frac{e}{D}\]
Here,
\[e= \text{Absolute Roughness}\]
Then the friction factor can be found through,
\[h_{L}= 4 f\times\frac{L}{D}\times\frac{V^{2}}{2g}\]
Here,
\[L= \text{Length of the pipe}\]
\[D= \text{Diameter of the pipe}\]
\[V= \text{Velocity of the flow}\]
\[g= \text{Gravitational Acceleration}\]
\[h_{L}= \text{Head Loss through a pipe}\]
\[f= \text{Friction Factor}\]
Normally for,
Laminar Flow: Reynolds number < 2000
Turbulent Flow: Reynolds Number > 4000
Point to be Noted:
- The absolute viscosity of all fluids is practically independent of pressure for the range that is ordinarily encountered in engineering work.
- The kinematic viscosity of gases changes due to the change of pressure because of changes in density.
References
- REFERENCES: FLUID MECHANICS WITH ENGINEERING APPLICATIONS – Robert L. Daugherty, Joseph B. Franzini

