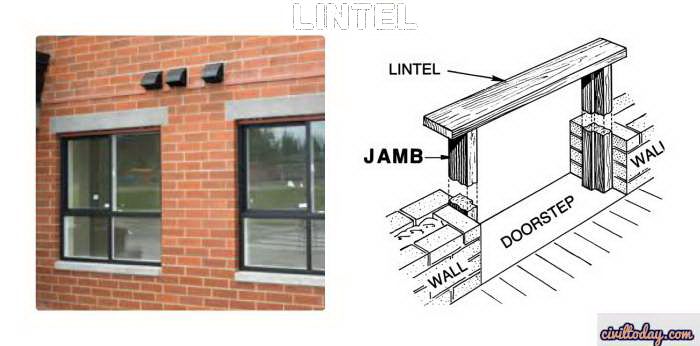
A lintel is a common part of buildings. Whenever we want to create an opening like doors & windows in the building, we use lintels above windows, doors like openings as a simple solution to support the weight above the opening.
Although lintel construction is simple and it is very commonly used, we are here to define lintel theoretically. Furthermore, we have presented 6 types of lintel beams here in this article and discussed them briefly to give you an idea. Why does this matter? It will help you to select the best kind of lintel for your lintels construction work and enable you to answer what are lintels.
What is Lintel? Lintel Definition
A lintel is one type of beam which is provided to support the above wall or partition material when openings like doors, windows, and so forth are necessary to provide a building structure.
Following is the lintels definition by Merriam-Webster to understand lintel meaning.
A flat horizontal beam that spans the space between two supports.
The lintel is an American word. In British English, it is called lintol. So don't be confused. Lintel and lintol both are the same words.
A lintel beam is a horizontal secondary structural element. It is mostly used above the openings on windows, doors, portals, fireplaces, etc. {adselite}
Lintel Construction Material
For lintel construction, different building materials can be used. Some lintel beam materials are listed below
- Reinforced cement concrete (RCC)
- Stone
- Wood/timber
- Bamboo
- Steel
What is a Lintel Used for? Uses or Functions of Lintels
The followings are the uses of lintel:
- The primary function of the lintel is to take loads originating from the wall directly above the opening and transfer them to the side walls or stone pillar support.
- Lintel also acts as a safeguard for the windows and doors.
- Continuous lintels may provide support in masonry structures against lateral loads like wind or earthquakes.
- The chimney above the fireplaces can be supported by lintels.
- Lintel can be used as a support for the canopy members.
- It is possible to enhance the architectural beauty of a building by selecting decorative lintels. lintel architecture would be a good matter of concern here.
- Lintels may support a small distance of a path. It could be referred to as a lintel bridge.
Properties of Lintel
The followings are the general properties of building lintel:
- The lintel beam generally ends in the masonry wall. Sometimes they are ends in the columns.
- Lintels must be supported at each end. They must be extended enough to ensure that the supporting masonry is stressed within their allowable stress. 100mm would be the minimum bearing length.
- Lintels convey the weight carried by them to the masonry walls.
- Lintel width is kept the same as the supporting wall width.
- The lintel can likewise be utilized as an enlivening compositional component.{adselite}
Lintel Beam Construction Guideline
Lintel design guidelines are specified in design codes. Before constructing a lintel one must follow the applicable codes of the country. Following are some general guidelines that may vary in different codes. It is highly recommended to follow the code applicable in your country rather than this guideline.
- 100mm minimum bearing length should be provided.
- A lintel span shall not exceed 3.5 m over openings.
- All concrete lintels shall be reinforced.
- The reinforcement bars of the concrete lintel beam shall extend more than 600 mm beyond the edge of the opening and into lintel supports.
Types of Lintels
While timber is as yet utilized in the development of homes, heavier materials, for example, block, concrete, and stone, can likewise be used, particularly in the event of business structures and private condo squares. Thus, the utilization of stirred steel lintels has developed increasingly well known. Depending on the cost and availability of materials, different materials are used for lintel construction. Lintel beams are classified into the following types according to the elements of their development:
- Timber lintel
- Stone lintel
- Reinforced concrete lintel
- Brick lintel
- Reinforced brick lintel
- Steel lintel
After seeing these six types of lintel you may ask a simple question.
Which one of these lintels should you use for your construction project?
It's you who should decide the answer. But to help you decide, a brief description of these six types of lintels is discussed below.{adselite}
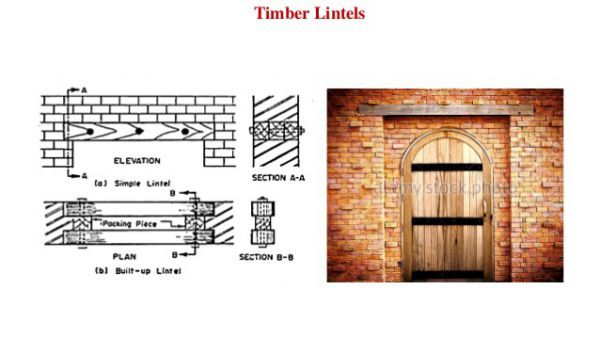
Timber Lintel
Wooden or Timber Lintels are the most seasoned sorts of lintel. They are fundamentally used in hilly areas where timbers are accessible. But in open areas, uses of timber are constrained as a result of the significant expense and accessibility of present-day materials. If there should be an occurrence of more great dividers, timber lintel beam is made out of two wooden pieces avoided as much as possible with the assistance of wooden separation pieces. Sometimes, timber lintels are reinforced by the arrangement of mild steel plates at their top and base; such lintels are called flitched lintels. It has a few other disadvantages-
- It is less durable.
- Timber being combustible it is vulnerable to fire.
- These lintels tend to be structurally weak.
- Without appropriate ventilation, timber is obligated to rot.
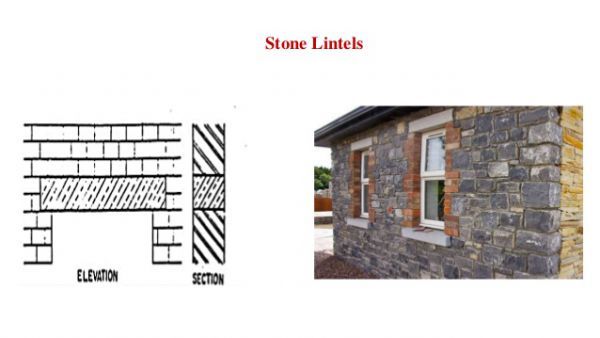
Stone Lintel
Rectangular bits of stone can be utilized as a lintel. This type of lintel is mainly used in this area where the stone is plentifully accessible. On the off chance that the length of the opening is long, by then, in any event, two bits of timber are joined to give the lintel all things considered openings. They are merely used in mountainous buildings as they weigh too much and due to the non-availability of other materials for their construction. Its use is intrinsically bound to stone masonry structures. Stone lintels must be utilized according to an understanding of the characteristic layering. The thickness of the stone lintel is a significant factor in its design. As a thumb rule, the thickness is taken as 4 cm. Per 30cm length of span and the minimum thickness should be 8 cm. This sort of lintel beam will be firm and solid. There are a few inconveniences also of the stone lintel.
- Its high cost and secondly its inability to withstand excessive transverse stress.
- Due to their weak tensile nature, they are not used in buildings where vibratory loads are subjected to the structure.
- It is difficult to deploy them in cities as transportation is a very complex task.
Reinforced Concrete Lintel
At present, reinforced concrete lintels are very common in use. In this type, reinforcement is used to overcome the low malleable issue in concrete. They are developed in present-day structures. They are suitable for heavy loads and larger spans. Their thickness is kept around up to 8 centimeters for every meter. RCC lintels can be either precast or cast in situ. Generally, precast reinforced cement concrete lintels are used when the lintel span is smaller. Lintel width should be the same as wall width. The depth of the lintel beam depends on the length of the span and the loading's magnitude.
Concrete, though strong in compression, is fragile to tensile stress, so main reinforcement bars are used at the bottom to resist the tensile stress. Half of these bars are cranked at the ends. Shear stirrups are provided to withstand shear stress. Typically, cement, sand, and aggregates are mixed in 1:2:4 ratio to form cement concrete mortar. This lintel has a handful of advantages:
- They are durable, rigid, and strong.
- The reinforced concrete lintel has fire-resisting properties.
- They are economical and easy to construct.
- The main advantage of the RC lintels is their adaptability to suit any size and shape.
Brick Lintels
Brick lintels are constructed with hard, well burnt first-class brick. It can be formed as bricks on the end, bricks on the edge, and coursed bricks laid horizontally over openings. This type of lintel is used when the opening is small (less than 1m) with light loadings. Their depth varies from 10 cm (thickness of one brick) to 20 cm depending upon the span. Bricks with frogs filled with mortar give more shear resistance at end joints than the standard blocks.
Reinforced Brick Lintels
Heavy loadings and more substantial span lengths are the problems for brick lintels. These can be overcome by using reinforcement bars. Reinforced brick lintels thus provide more support than brick lintels. The depth of the reinforced brick lintels is equal to 10 cm. or a multiple of 10 cm (or one brick thickness). The arrangement of the bricks should be such that there is enough space lengthwise between the adjacent bricks for the insertion of mild steel bars as reinforcement. After insertion bars, the remaining gap is filled with 1:3 cement mortar. 6 mm bars are used as vertical stirrups at every 3rd vertical joint. 8 to 10 mm bars placed at the bottom are used as primary reinforcement.
Steel Lintels
A steel lintel beam can be suitable when the superimposed loads are heavy, and the opening gaps are significant. Steel lintels are preferable when the depth of lintel plays an essential role because the designer cannot ignore the depth of reinforced concrete lintels due to heavy loads. These lintels consist of channel sections or rolled steel joists or channel sections either used singly or in the combination of two or three units. Depending upon the requirements, the lintel can be a single section or a combination of two or more. A single steel joist is either embedded in concrete or cladded with stone facing to keep the same width as the wall. A combination of two or more units is placed side by side and held in position by a tube separator. Relieving with water is accomplished in any event for ten days. It has many advantages:
- Steel lintels can be utilized to help heavier loads over more prominent separations without the need to change or strengthen.
- They are impervious to rust, erosion, or distortion.
- Steel lintels are more practical and less labor-intensive.
FAQs
What is the difference between lintel and beam?
Lintel and beam are both horizontal building members. A member is identified between these two names based on its function.
lintel supports only the weight of the wall above the openings and it transfers the load to walls only.
Whereas beams carry the dead and live load from the slab. These loads are then transferred to the supporting columns. Also beams act as diaphragm elements.
What is meant by door lintel? What is a door lintel?
A horizontal beam that is positioned across a door opening to bear the load of the structure above it is designated a door lintel.
Do you need a lintel above a window?
If brick walls or other heavy nonstructural members exist between the window and the structural beam above, a lintel is mandatory above a window. This window lintel will distribute the loads to the masonry wall beside the window. Window lintels can also secure the window frame from damage.
What is a window lintel?
The horizontal structural member constructed above the window to support the brick wall above is called a window lintel.
When Do you need a garage door lintel replacement?
Garage door lintel replacement is not typically recommended unless the door itself is severely damaged. If the garage door is only slightly bent or has a small hole, then a new lintel may be all that is needed. If the garage door is severely damaged, a new door may be the only solution.
That’s not all !!!!!!
Here is the list of lintel articles on our website
- What is Lintel? Types of Lintel
- Purposes of a Lintel Beam
- Functions of Lintel Beam
- Lintel Beam Design Loads
More lintel articles are coming soon...
If brick walls or other heavy nonstructural members exist between the window and the structural beam above, a lintel is mandatory above a window. This window lintel will distribute the loads to the masonry wall beside the window. Window lintels can also secure the window frame from damage.

